News   Newsletters   Interviews   Gallery   Grades   Competitions   Tick Lists   Guides   Grants   Links   Contact Us 

Elementary grading: 1 + 1 = 3.   By Kyle Dunsire

Nobody would argue that grading boulder problems is a tricky business; subjective, inconsistent and prone to variation. But, throw in sit-starts and traverses, and things really seem to go pear-shaped. But fret not – here is the AB.C guide to understanding ‘compound grades’.

‘Compound problem’ is the term I’m using to describe what you get when you join two existing problems (or distinct sections) together. Logically, you get one problem with a compound grade. Ok, but how do you know or calculate what that grade should be?

The important point to realize is that sometimes the grade should be unaffected. Just because you add a few moves to an existing problem doesn’t make it harder. For example, climbing a V9 with a V5 extension doesn’t necessarily make it V10. Sure, it’s harder than the V9 alone, but not enough to warrant an extra grade (even if you fall off the extension a few times).

The rule of thumb that we use at AB.C is this: the addition of two boulder problems of the same grade equates to one boulder problem of the grade +2. So a V9 into a V9 should produce a V11. Everything else works around that premise. The following examples (based on V9) should help convey the idea:

V9 + V6 = V9,
V9 + V7 = V10,
V9 + V8 = V10,
V9 + V9 = V11,
V9 + V10 = V11,
V9 + V11 = V12,
V9 + V12 = V12

Note: You can generate this table by adding the grades together, adding 4 and then dividing by 2 – but that’s all a bit mathematical.

Before you start e-mailing your complaints, be aware that this is a somewhat heuristic approach, and shouldn’t be construed as rigid. So, yeah, in some cases a V9 into another V9 may actually only be V10. Consider, however, the following illustrative (and grade-confirmed) cases:

Consider what happens with longer problems and traverses. A lot of people believe that traverse grades are softer than bloc (straight up). Actually, the grade scale is equivalent, but it’s showing its limitations. Consider a long sequence of easy moves which is given the same grade as a single hard one. Obviously the one move must be ‘harder’ than any of the moves on the longer problem. Therefore the long sequence is in a sense ‘easier’. See the dilemma? I would argue that more people could do the long sequence than the one move problem, since it boils down to efficiency.

Consider the famous Cave Rave in the Hollow Mountain Cave. Using our rule of thumb we would expect a grade of V9 + V11 = V12 (in theory), but it has been graded V13/14. Why the discrepancy? Because the problems are relatively long – 15 moves or so. Endurance starts to become a real issue, even though there are large jugs linking the problems. It’s more like climbing a sustained route with a hard crux at the end than a boulder problem. The point I’m illustrating here is that a problem can be graded higher, simply because of the length. This distorts the discrepancy between bloc and traverse grades even more.

When Fred Nicole was asked to comment on the grade of Cave Rave, he was hesitant about using a bouldering grade. He thought it was more accurately termed a ‘route without a rope’, and should be given a route grade accordingly (34?). In the end, it gets the grade it does because two great climbers took significant time and effort to do it… about a V13 or 14’s worth.

What does all of this prove? Well, as I said at the start, it’s a tricky business.

Grade Theory? by Tim "send your flaming emails here" O'Neill

For all those that are squeamish about grades click here for something a little more palatable!  Otherwise, read on ...

The following histogram gives you a summary of the number of sends for each V10+ grade in Australia.  Now before you flame me about being elitist, you try and imagine counting how many V3's have been sent in the history of Australian bouldering ... I'm anal but not THAT anal :)

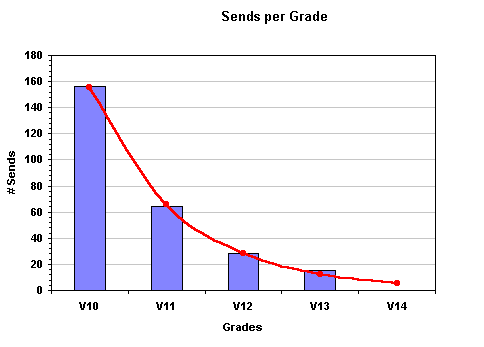
You can see that there are (as one would expect) progressively less sends per grade as the grade increases.  In measurement theory this means that the V system is reassuringly at least "ordinal" (ie. V12 is harder than V11 etc).  The obvious observation is that there are about half as many sends of each successive grade as the previous.  This should mean that each successive grade can be considered as about twice as hard.  Well at least that only half as many people should be able to climb it.

Now, there is actually a very elegant relationship between the number of sends per grade and this is shown with the red trendline above.  This relationship is;

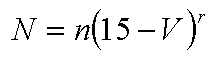
Where;

N = numbers of sends per V grade (the Y axis).

V = the V grade (V13 = 13, V12 =12 etc - the X axis)

n = 2.17 a scaling constant that reflects the popularity of/population in Australia.

r = 2.35 a relative constant that reflects the difference in difficulty of each successive grade.

So, it seems that each grade is actually 2.35 times as hard as the previous (as opposed to the general heuristic of twice).  The scaling constant of 2.17 really just reflects how popular bouldering is in Australia.  As we develop and repeat more problems one would expect that the scaling constant would just increase, NOT the relative constant.  Of course, if we start over or under-grading problems (compared to what we've done in the past that is) then this number would change as well.  We could also compare these constants with other countries to see where bouldering is the most popular and to see how they compare wrt over or under-grading.  It'll be interesting to see, well for me at least ...

So how does this help us to grade our latest projects?  The short answer is ... errr ... "not sure" but slowly we're developing some good heuristics (read the "add 21" rule below) to hopefully help us.  Any researchers out there looking for a research project ...

Tim O'Neill

Grade Conversion

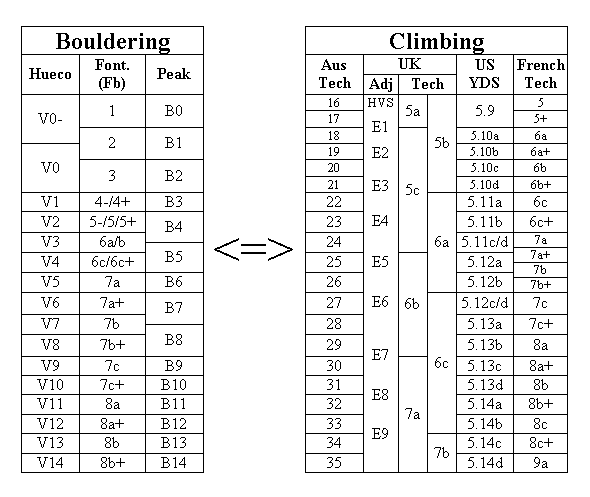
So you can see from these tables that my rough rule is "add 21". This of course is from the Hueco bouldering grade to the Ewbank climbing grade. This is to be interpreted as if you can boulder V5 then you can probably climb 26. A good justification for this is that the hardest boulder problems in the world are V14 and the hardest routes are 35 and these are being put up by the same people (ie. Fred and Klem et al). Now I know that you then have the "power mutant" vs "pumper" issues and obviously a pumper will be add >21 and a power mutant will be add <21 but it seems to fit in general. I must point out that this doesn't mean that a grade 26 has V5 moves on it. While it could it typically would involve more moves or lesser difficulty, say V3? For example, Klem describes Vakuumgeist which is French 9a or Ewbank 35 as 2 V12's. More close to home, Eve Ręve is a link-up of a V10 (Cave man) into a V12 (Dead can't dance). So you can see that 35's involve V12 moves not V14 moves and if you can climb 35 you can probably boulder V14 and your name is Fred or Klem :)